Transpalindromes

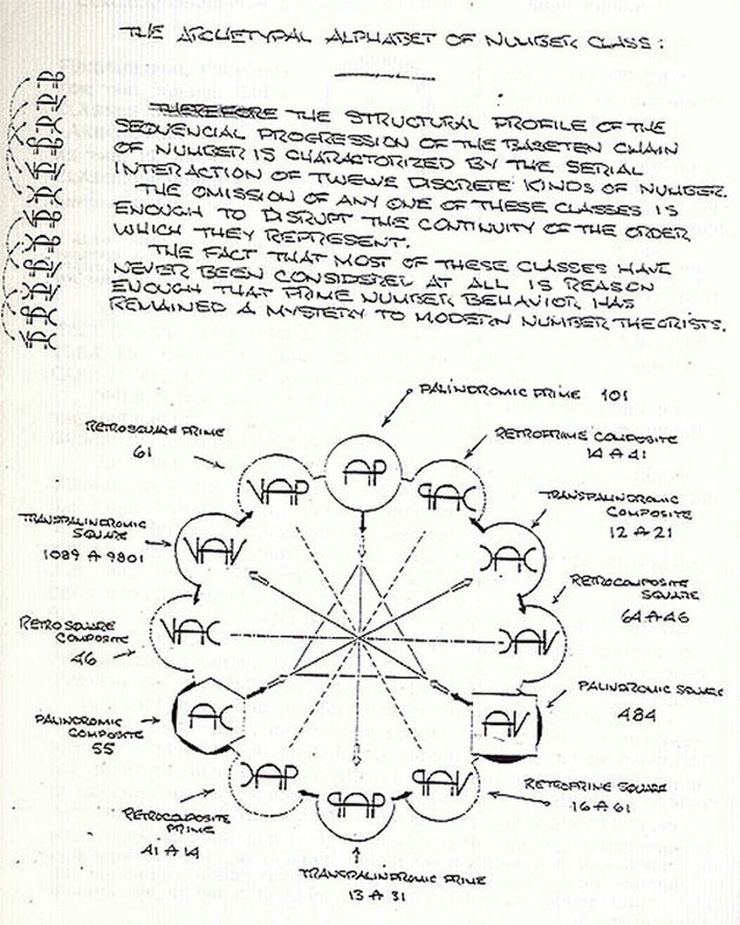
Transpalindromicity of number is merely a term by which we include the reversal of any particular number exceeding a single digit. For example, 16 and 61.
Another example involving a transpalindromic distinction is when a reversed number remains in its class, like 13 and 31 which are both primes, i.e. transpalindromic primes as compared to a simple palindromic prime such as eleven. These are only twelve permutations possible within the whole continuum of number.
The complete analysis of number behavior is not possible without taking into account the palindromic and transpalindromic characters of number. This is the crucial and paramount reason that the behvaior of prime numbers have remained an enigma for so long.
Number theory has ignored the ambidirectional reflexivity inherent in the number continuum. Regaining an impartial view of how reflexivity is totally conserved within the continuum leaves no gaps in the concept of numerical continuity.
The synchrographs and mandalogs used in this study are to support the continuity that has been disrupted by the belief that prime numbers are without connective order. Toward this end, we introduce approximately 16 new words that fill in the missing blanks to form a coherent picture or concept of true number dynamics.
The term "synchrostat" designates an event synchronicity in the numeric continuum. This term and its subsequent Tables were valuable tools in indentifying a cyclic series of numbers that embody features that were common to all members of the series. They embody and exemplify a practice that was used to explore many other cycles until the main base cycle was finally discovered.
Synchrostat illus. here.
Comprehending the universal nature of the transpalindromic function of number behavior is not easy. We tend to see the number chain as a unidirectional continuum, which is too linear for a synergetic perspective. Revisioning it with the concept of simultaneous counterflow yields a more accurate picture. With large spans of number, the complex interrelationships become difficult to visualize.
Fortunately, because of the octave nature of the base cycle there cannot be more than four consecutive transpalindromic pairs in a single symmetrical sequence, regardless of the amount of digits in each individual number.
However, we are only looking at the multiples of nine. But, in fact, all the numbers in between are also involved in transpalindromic transactions. To address such a complex interchange by graphic means can only be accomplished in a series of static cross-sections each involving no more than the eight required transactions.
The exemplary 99 wavecycle affords us a context that gives a graphic expression of total transpalindromic symmetry which it is possible to contemplate with clarity.
All the Holotomes contain the same general mechanism seen in the 99 cycle, but even the Holotomes must be contemplated in various graphic modes to capture their full integrity.
Transpalindromicity functions through the ambidirectional nature of number. It is therefore, the initial or primary function of number behavior in general. All details of number behavior derive primarily from a transpalindromic function operating through an ambidirectional chain of ambidirectional numerical events.
If any aspect of direction is left unconsidered in the behavior of any specified event then behavior observed in connection with that event will have been compromised. In the past, there has been a general disregard for the retrocity of number in general. Yet, no single function is more important or interesting than this transpalindromic nature in determining the basic waveforms inherent in baseten numeration.
Transpalindromic symmetry refers to a circular module of numerical relationships and interoperations which form a totally harmonious retrograde and symmetrical octave unity. The emphasis is not on palindromes, but on the relationship existing between palindromes and transpalindromes:
1089
Palindromes: 55 x 99 = 5445
9018
We can take any number, reverse it, add the two numbers together, continue to reverse and add, and eventually end up with a palindrome--a number whose digits appear in the same order whether they are read from left to right or from right to left.
Transpalindromic symmetry is not isolated to the few graphic expressions submitted here as examples to clarify the meaning of this neologism (transpalindromicity) on the subject of number behavior.
Transpalindromic behavior itself is a totally general condition of the number chain and is operative throughout the continuum. It is also a primary factor in the graphic disclosure of many subtle but important aspects of number behavior; an intrinsic structural condition effecting every and all numbers in their collective interactions.
Transpalindromic symmetry is a condition relating to specific isolated groups of number or special numerical quata where symmetry manifests as a collective mutual interaction.
A Holotome is such a collective interactive group where symmetry is herein claimed to be absolute.
A Holotome is distinguished by an integrity of retrograde octave symmetry, discrete levels of finitude and circular unity. Its expression in synchrographic form is a holistic synthesis of graphic syntax.
A contemplative instrument of inquiry into the relationships between words and the idea-pictures they mean to represent.
Transpalindromic symmetry means cycloreflexive synchronicity: what comes around goes around. Palindromes are symmetrically flanked by up to four tranpalindromic pairs.
SUMMARY
The Goldbach Postulate alleges that 'every even number is the sum of two primes.' The case has not yet been reported where this does not hold true. Even though this postulate is unprovable in the sense that all even numbers can't be checked out, it may be provable through a true understanding of how the sequence of number operates.
No even number may be a prime because of the prior occurrence of number 2, which acts as a divisor for all even numbers. The first three odd numbers are primes because no number preceding them has occurred that could act as a divisor. Number 9 is the first odd number that is not a prime, because of the prior occurrence of number 3.
Therefore, the occurrence of the first odd number as a composite is the result of the previous occurrence of an odd number that had no preceding divisors except unity, which is indivisible by definition. So, the composite nature of 9 is causally determined in that 9 would have been a prime like all previous odd numbers, but for the prior occurrence of number 3.
From this it may be postulated that all even numbers will be composites, and all odd numbers are potentially primes unless some previous odd number has occurred that acts as a factor, rendering them composites.
This is also a way of saying that every odd number that is not a prime is the product of at least one previous prime and one previous composite, (3 + 6 = 9).
But the serial equatability of the of the progressively divisible number chain produces a surplus of combinations to produce primes from even numbers. In fact, as numbers progress, composites will occur that accomodate multiple sets of primes and visa versa, rendering the Goldbach Postulate a probability.
The assumption that all odd numbers would be primes if no previous number had occured that would act as a divisible factor perfectly fits the case. If the prior number had not occured, or could be stricken out, as in the case of number three, 9 would be a prime number, but sincle three is three and not something else, 9 is a composite.
The fact that nine is also a square number tells us also that the generation of squares, cubes, etc. is also a result of the occurrence of previous odd numbers, as two odds make and even and two of the same odd numbers multiply into a square number.
Continuity is a provisional term that requires a context describing a series of entity events that connect or disconnect to or from each other.
The primes have always been regarded as a single class with no breakdown into sub-classes, no different kinds of primes.
Secondly, the primes have been viewed apart from the composites, thereby ignoring any relationships that they certainly must share with other classes of number.
The first indications that other classes of primes exist was found in the nature of square numbers. The square number sixteen contains unique features when reversed to 61, as we have noted elsewhere.
All consecutive primes between 0 and 1000 differ from each other by even numbers which range from 2 to 20 with one exception: none differ from each other by 16, reflecting our exceptional 2-digit prime/square reversal.
The first three digits--1,2, and 3--are generally regarded as primes, but the initial members are in a class by themselves. One is not even a number, in the serial sense. It does not multiply like real numbers do. Two is also not a number, but the source of doubling of unity--duality. 1 x 2 is 2 x 1. It is the source of duality, eveness or balanced symmetry, and essentially static state.
Three is also not a number, but the source of imbalance and asymmetry, a source of dynamic flow. The source of oddity or difference with these three qualities produces number four, the first real number or the idea of quantity/quality and dimensionality of the tetrahedron.
Even and odd are established in the ideas of two and three. They are essentially spatial or geometrical ideas relating to shape and form. They are the prototypes that establish the classes of number yet to come.
All even numbers are non-primes because they are matched pairs or symmetrical sets of two.
All odd numbers are potentially primes, being uneven non-symmetrical amounts. The first odd number to become a composite is nine. It is not a prime because of the initial occurrence of 3, which acts as a factor making 9 geometrically symmetrical. Two odds make an even. 9 is axially odd, but radially even.
The SYNDEX description of number behavior employs the overview of the cycloflex. It represents the reality of function that is both cyclic and oscillatory, i.e. both rotational and reciprocating.
In describing number behavior and dynamics, it becomes necessary to show the interaction existing between palindromic and transpalindromic numbers--an interaction that is in essence a cyclic behavior.
The retrograde functions progress to a point and then reverse in octave cycles of four forward and four backward number events. This is a wave-cycle or cycloflex.
Continuity in the description of the exemplary basewave cannot mean it in the sense of something uninterrupted because it must be curtailed on the upper limit of the Holotome for the sake of holistic unity.
Continuity has given trouble to the number theorist because of the mind's insistance that any specific integer is an isolated idea entity and cannot be effected by another integer, several or even many times removed. But this is, in reality, the case when number 9 is not a prime because of the usurpation of its "primeness" by 3.
This transinteger dynamic is a passive dynamic. It happens as an acausal determinate which means the retrograde loops on the SYNDEX number maps are left to show the truth.
The number reversals that purport to carry the exemplary wave are gestures of quasi-disconnective continuity because the relations must be shown that we may see how numbers interact as they flow towards some "nothing" called infinity.
The prior reference to approach of holistic continuity at the end of a Holotome is the final non-event of such a specific system. The octave is best deactivated at these discrete points. It is predominantly the Holotomes that clarify the distribution of prime numbers, for the primes are symmetrically arrayed within the context of each holotome.
The radial symmetry of the holtomes is, in itself, the geometrical proof of numerical coherency. That each subsequent holotome admits one, and only one, additional divisor establishes a rational medium between prime numbers and the sequence of specific compositry.
Though the structure of the baseten continuum is a highly complex order, there are graphic methods by which the more important aspects of that order may be appreciably simplified.
For example, there are very rare, often unique examples, of certain classes of number that occur seldom or even just once in the two-digit numbers and it was through the discovery of these rare or noble examples that the exemplary basewave cycle was discovered. Once that cycle was isolated, it was a simple matter to extrapolate into the higher order to secure the multiple digit cousins of those noble examples for comparisons to confirm the sustained functions of the cycles being investigated.
A basewave was long ago suspected by the classical number theorists, but its elusive nature was due to the fact that it was not a singular wave form but a compound variety. A wave composed of the mutual interaction of square number nine and prime number eleven whose essential palindromic nature is connected with the transpalindromic aspects of the total numeric profile.
The Synchrographs act as maps by which we may follow the progress of this exemplary wave cycle. It is a feature that would not in any way be apparent without such a systematic graphic mechanism.
The nineleven wave is further caged by such features of the continuum as the line pair of 4-digit transpalindromic squares--those being the square of 33 and 99: 1089 and 9801. These two interreflecting squares neatly bracket an octave sequence of four forward and four reverse multiples of the first square which significantly includes a center or nave member which is a palindrome which results from two 2-digit palindromes.
By and large, it is predominantly the holotomes that clarify the distribution of prime numbers because the primes are symmetrically arrayed within the context of each holotome. And the number of primes in each holotome is determined by the total modular amount of the previous holotome. For example, Holotome E or #2520 contains 367 primes or just seven more than Holotome D which is #360 (360 x & = 2520) and Holotome D contains 72 primes, where #72 is the modular sum of the previous holotome.
The fundamental intent of the initial ideas was to create a context which would geometrically paraphrase the elements of numerical progression in a graphic system that involves the primary elements of plane or two dimensional geometry. The two axes provide a base for symmetry as a reference to systematically involve the cyclic and wave functions of the numeric continuum.
Another example involving a transpalindromic distinction is when a reversed number remains in its class, like 13 and 31 which are both primes, i.e. transpalindromic primes as compared to a simple palindromic prime such as eleven. These are only twelve permutations possible within the whole continuum of number.
The complete analysis of number behavior is not possible without taking into account the palindromic and transpalindromic characters of number. This is the crucial and paramount reason that the behvaior of prime numbers have remained an enigma for so long.
Number theory has ignored the ambidirectional reflexivity inherent in the number continuum. Regaining an impartial view of how reflexivity is totally conserved within the continuum leaves no gaps in the concept of numerical continuity.
The synchrographs and mandalogs used in this study are to support the continuity that has been disrupted by the belief that prime numbers are without connective order. Toward this end, we introduce approximately 16 new words that fill in the missing blanks to form a coherent picture or concept of true number dynamics.
The term "synchrostat" designates an event synchronicity in the numeric continuum. This term and its subsequent Tables were valuable tools in indentifying a cyclic series of numbers that embody features that were common to all members of the series. They embody and exemplify a practice that was used to explore many other cycles until the main base cycle was finally discovered.
Synchrostat illus. here.
Comprehending the universal nature of the transpalindromic function of number behavior is not easy. We tend to see the number chain as a unidirectional continuum, which is too linear for a synergetic perspective. Revisioning it with the concept of simultaneous counterflow yields a more accurate picture. With large spans of number, the complex interrelationships become difficult to visualize.
Fortunately, because of the octave nature of the base cycle there cannot be more than four consecutive transpalindromic pairs in a single symmetrical sequence, regardless of the amount of digits in each individual number.
However, we are only looking at the multiples of nine. But, in fact, all the numbers in between are also involved in transpalindromic transactions. To address such a complex interchange by graphic means can only be accomplished in a series of static cross-sections each involving no more than the eight required transactions.
The exemplary 99 wavecycle affords us a context that gives a graphic expression of total transpalindromic symmetry which it is possible to contemplate with clarity.
All the Holotomes contain the same general mechanism seen in the 99 cycle, but even the Holotomes must be contemplated in various graphic modes to capture their full integrity.
Transpalindromicity functions through the ambidirectional nature of number. It is therefore, the initial or primary function of number behavior in general. All details of number behavior derive primarily from a transpalindromic function operating through an ambidirectional chain of ambidirectional numerical events.
If any aspect of direction is left unconsidered in the behavior of any specified event then behavior observed in connection with that event will have been compromised. In the past, there has been a general disregard for the retrocity of number in general. Yet, no single function is more important or interesting than this transpalindromic nature in determining the basic waveforms inherent in baseten numeration.
Transpalindromic symmetry refers to a circular module of numerical relationships and interoperations which form a totally harmonious retrograde and symmetrical octave unity. The emphasis is not on palindromes, but on the relationship existing between palindromes and transpalindromes:
1089
Palindromes: 55 x 99 = 5445
9018
We can take any number, reverse it, add the two numbers together, continue to reverse and add, and eventually end up with a palindrome--a number whose digits appear in the same order whether they are read from left to right or from right to left.
Transpalindromic symmetry is not isolated to the few graphic expressions submitted here as examples to clarify the meaning of this neologism (transpalindromicity) on the subject of number behavior.
Transpalindromic behavior itself is a totally general condition of the number chain and is operative throughout the continuum. It is also a primary factor in the graphic disclosure of many subtle but important aspects of number behavior; an intrinsic structural condition effecting every and all numbers in their collective interactions.
Transpalindromic symmetry is a condition relating to specific isolated groups of number or special numerical quata where symmetry manifests as a collective mutual interaction.
A Holotome is such a collective interactive group where symmetry is herein claimed to be absolute.
A Holotome is distinguished by an integrity of retrograde octave symmetry, discrete levels of finitude and circular unity. Its expression in synchrographic form is a holistic synthesis of graphic syntax.
A contemplative instrument of inquiry into the relationships between words and the idea-pictures they mean to represent.
Transpalindromic symmetry means cycloreflexive synchronicity: what comes around goes around. Palindromes are symmetrically flanked by up to four tranpalindromic pairs.
SUMMARY
The Goldbach Postulate alleges that 'every even number is the sum of two primes.' The case has not yet been reported where this does not hold true. Even though this postulate is unprovable in the sense that all even numbers can't be checked out, it may be provable through a true understanding of how the sequence of number operates.
No even number may be a prime because of the prior occurrence of number 2, which acts as a divisor for all even numbers. The first three odd numbers are primes because no number preceding them has occurred that could act as a divisor. Number 9 is the first odd number that is not a prime, because of the prior occurrence of number 3.
Therefore, the occurrence of the first odd number as a composite is the result of the previous occurrence of an odd number that had no preceding divisors except unity, which is indivisible by definition. So, the composite nature of 9 is causally determined in that 9 would have been a prime like all previous odd numbers, but for the prior occurrence of number 3.
From this it may be postulated that all even numbers will be composites, and all odd numbers are potentially primes unless some previous odd number has occurred that acts as a factor, rendering them composites.
This is also a way of saying that every odd number that is not a prime is the product of at least one previous prime and one previous composite, (3 + 6 = 9).
But the serial equatability of the of the progressively divisible number chain produces a surplus of combinations to produce primes from even numbers. In fact, as numbers progress, composites will occur that accomodate multiple sets of primes and visa versa, rendering the Goldbach Postulate a probability.
The assumption that all odd numbers would be primes if no previous number had occured that would act as a divisible factor perfectly fits the case. If the prior number had not occured, or could be stricken out, as in the case of number three, 9 would be a prime number, but sincle three is three and not something else, 9 is a composite.
The fact that nine is also a square number tells us also that the generation of squares, cubes, etc. is also a result of the occurrence of previous odd numbers, as two odds make and even and two of the same odd numbers multiply into a square number.
Continuity is a provisional term that requires a context describing a series of entity events that connect or disconnect to or from each other.
The primes have always been regarded as a single class with no breakdown into sub-classes, no different kinds of primes.
Secondly, the primes have been viewed apart from the composites, thereby ignoring any relationships that they certainly must share with other classes of number.
The first indications that other classes of primes exist was found in the nature of square numbers. The square number sixteen contains unique features when reversed to 61, as we have noted elsewhere.
All consecutive primes between 0 and 1000 differ from each other by even numbers which range from 2 to 20 with one exception: none differ from each other by 16, reflecting our exceptional 2-digit prime/square reversal.
The first three digits--1,2, and 3--are generally regarded as primes, but the initial members are in a class by themselves. One is not even a number, in the serial sense. It does not multiply like real numbers do. Two is also not a number, but the source of doubling of unity--duality. 1 x 2 is 2 x 1. It is the source of duality, eveness or balanced symmetry, and essentially static state.
Three is also not a number, but the source of imbalance and asymmetry, a source of dynamic flow. The source of oddity or difference with these three qualities produces number four, the first real number or the idea of quantity/quality and dimensionality of the tetrahedron.
Even and odd are established in the ideas of two and three. They are essentially spatial or geometrical ideas relating to shape and form. They are the prototypes that establish the classes of number yet to come.
All even numbers are non-primes because they are matched pairs or symmetrical sets of two.
All odd numbers are potentially primes, being uneven non-symmetrical amounts. The first odd number to become a composite is nine. It is not a prime because of the initial occurrence of 3, which acts as a factor making 9 geometrically symmetrical. Two odds make an even. 9 is axially odd, but radially even.
The SYNDEX description of number behavior employs the overview of the cycloflex. It represents the reality of function that is both cyclic and oscillatory, i.e. both rotational and reciprocating.
In describing number behavior and dynamics, it becomes necessary to show the interaction existing between palindromic and transpalindromic numbers--an interaction that is in essence a cyclic behavior.
The retrograde functions progress to a point and then reverse in octave cycles of four forward and four backward number events. This is a wave-cycle or cycloflex.
Continuity in the description of the exemplary basewave cannot mean it in the sense of something uninterrupted because it must be curtailed on the upper limit of the Holotome for the sake of holistic unity.
Continuity has given trouble to the number theorist because of the mind's insistance that any specific integer is an isolated idea entity and cannot be effected by another integer, several or even many times removed. But this is, in reality, the case when number 9 is not a prime because of the usurpation of its "primeness" by 3.
This transinteger dynamic is a passive dynamic. It happens as an acausal determinate which means the retrograde loops on the SYNDEX number maps are left to show the truth.
The number reversals that purport to carry the exemplary wave are gestures of quasi-disconnective continuity because the relations must be shown that we may see how numbers interact as they flow towards some "nothing" called infinity.
The prior reference to approach of holistic continuity at the end of a Holotome is the final non-event of such a specific system. The octave is best deactivated at these discrete points. It is predominantly the Holotomes that clarify the distribution of prime numbers, for the primes are symmetrically arrayed within the context of each holotome.
The radial symmetry of the holtomes is, in itself, the geometrical proof of numerical coherency. That each subsequent holotome admits one, and only one, additional divisor establishes a rational medium between prime numbers and the sequence of specific compositry.
Though the structure of the baseten continuum is a highly complex order, there are graphic methods by which the more important aspects of that order may be appreciably simplified.
For example, there are very rare, often unique examples, of certain classes of number that occur seldom or even just once in the two-digit numbers and it was through the discovery of these rare or noble examples that the exemplary basewave cycle was discovered. Once that cycle was isolated, it was a simple matter to extrapolate into the higher order to secure the multiple digit cousins of those noble examples for comparisons to confirm the sustained functions of the cycles being investigated.
A basewave was long ago suspected by the classical number theorists, but its elusive nature was due to the fact that it was not a singular wave form but a compound variety. A wave composed of the mutual interaction of square number nine and prime number eleven whose essential palindromic nature is connected with the transpalindromic aspects of the total numeric profile.
The Synchrographs act as maps by which we may follow the progress of this exemplary wave cycle. It is a feature that would not in any way be apparent without such a systematic graphic mechanism.
The nineleven wave is further caged by such features of the continuum as the line pair of 4-digit transpalindromic squares--those being the square of 33 and 99: 1089 and 9801. These two interreflecting squares neatly bracket an octave sequence of four forward and four reverse multiples of the first square which significantly includes a center or nave member which is a palindrome which results from two 2-digit palindromes.
By and large, it is predominantly the holotomes that clarify the distribution of prime numbers because the primes are symmetrically arrayed within the context of each holotome. And the number of primes in each holotome is determined by the total modular amount of the previous holotome. For example, Holotome E or #2520 contains 367 primes or just seven more than Holotome D which is #360 (360 x & = 2520) and Holotome D contains 72 primes, where #72 is the modular sum of the previous holotome.
The fundamental intent of the initial ideas was to create a context which would geometrically paraphrase the elements of numerical progression in a graphic system that involves the primary elements of plane or two dimensional geometry. The two axes provide a base for symmetry as a reference to systematically involve the cyclic and wave functions of the numeric continuum.